One solution to "=IRR generates a #NUM! error"

joeu2004 responded to this post, but for some reason, it is not shown. He demonstrated that large numbers can work and asked me to post one of my failed cashflows to a sharing website. Since my cloud sites I don't think allow general sharing, I have pasted one of the cashflows below. The left column are the full numbers and the right divided by one million. Numbers to the right of the decimal points are omitted. While this example generates a negative IRR, the same problem occurs with positive results. However, when I round the numbers, eg, by pasting them back from this post, IRR generates correctly for both series. Seems curious.

By "valid", I mean NPV(B45,B46:B70) returns about 7.20E-05, which is close enough to zero, especially considering the magnitude of the cash flows.

You might ask:  Why -4.65% instead of -5%?

Well, perhaps you chose -5% because you discovered that NPV(-10%,...) is positive and NPV(0,...) is negative.  So it is reasonable to choose the midpoint, -5%.

But when IRR(...,-5%) still returns #NUM, I would drill down further.  NPV(-5%,...) is positive and NPV(-4%,...) is negative.  So try IRR(...,-4.5%).  Unfortunately, that still returns #NUM.  Drill down further.  NPV(-4.7%,...) is positive and NPV(-4.6,...) is negative.  So try IRR(...,-4.65%).  Bingo!

To be sure, that process might not always work.  Sometimes, Excel IRR cannot find a solution within the limitations of its algorithm.  Sometimes, there is no IRR mathematically (!).  Or we might simply give up trying to find a workable "guess" after several "drill down" iterations.

-----

You might still ask:  Why does IRR(...,-5%) work when the cash flows are divided by 1,000,000?  (And I mean the exact division, not rounded to integers.)

I'm not sure.  I have an inkling for why the Excel IRR is sensitive to the magnitude of the cash flows.  But frankly, I'm not taking the time to explore it.

(Certainly, there are 64-bit binary floating-point limitations that limit the cash flow magnitude. But I do not believe your cash flows are affected by those limitations, especially when we provide a "guess".)

FYI, my own Newton-Raphson implementation (myIRR) does not require a "guess" at all (!).

I believe the difference is:  I use the exact derivative of the NPV equation, whereas I suspect Excel IRR uses an approximate derivative, perhaps using Newton's Difference Quotient.

Thanks Joeu.

In my series, even when I guess  -0.0465377 (the exact answer based on my series divided by one million) it does not work.

As I mentioned in my first post, in another series the ninth year cash flow is +279000000 when the series generates an error. If I change the figure to 279000000.1, it generates IRR correctly. This seems totally weird - how could 0.1 in 279 million have any impact?

I have 4 projects to assess each with around 6 IRR calcs (eg, for sensitivity testing), and your guessing option sadly does not work for me (see above). However dividing by 1,000,000 does, so that seems to be the best and quickest bet. Maybe Microsoft can work it out. I have entered the same info onto UserVoice. We'll see.

First, I meant to say:  you might get different results because I am using Excel 2007, and I believe Excel (X)IRR was "improved" starting with Excel 2010.

Second, -0.0465377 [sic] does not work for me, either.  Note that I wrote -4.65%.

You would think that a closer "guess" would work as well, if not better. It does not.  But that has little to do with magnitude of the cash flows.  I have experienced that with "normal" cash flows, too.  Again, I speculate that it is because Excel (X)IRR estimates the derivative, instead of using the exact derivative.

Third, interestingly, although -4.65% works for me, -0.0465 does not (!).  There is a binary difference; but it is only a difference of 1 in the least-significant bit.  So I suspect it is just "dumb luck" that -4.65% works for me.

(Although -4.655% also works for me.  I had originally tried -4.655% because I discovered that NPV(-4.66%,...) is positive and NPV(-4.65%,...) is negative.)

Anyway, I'm glad that you posted to uservoice.com.  I added my vote and some comments.

> ... However dividing by 1,000,000 does, so that seems to be the best and quickest bet.

Hi.  I can't add much because we will never know what algorithem Excel is using.
Custom functions work much better.
However, we can make some interesting observations about your data that may be worth mentioning.

First thou, Excel 2016 returned a pretty accurate value for both the windows and Mac version.
However, there are still many problems like this that do return Num Errors.

> ... "I increased the number of permitted iterations (to >1000) and the Maximum Change, with no effect."

If I am not mistaken, I don't believe IRR uses this option.  It uses it's own iteration.  Note from help:

"...until the result is accurate within 0.00001 percent. If IRR can't find a result that works after 20 tries, the #NUM! error value is returned."


If we look at your cash flows, we see that the total positive returns "never" exceed the initial investment.  Without doing anything, we see that this is a terrible investment.  We know from the start that the return value will be negative.  

What generally happens on the negative side of the x axis, (the rate), is that the slopes are usually very large.
Note that as r approaches -1,  the value tends towards infinity   ( x / (1+r)  )

If we look at the derivative of the equation at our solution of -.0465.., we see a slope of about -1.5 E12
This is very large.  Almost vertical.  A very small change in r results in a very large change in output.   This makes it much harder to solve for a value at zero.
I believe this is why Excel's poor algorithm "usually" has a hard time on this side of the axis.

When we divide the cash flows by 1,000,000 ,  we do not change the solution of r.  However, we do change the derivative by a large amount.  The new value is about -1.5 E6

This makes it "more likely" to be able to narrow in on a solution faster than with the larger values.


An interesting side note is that if you plug your accurate value of r into the equation for cash flows, I get a value of 0.000082.
This is basically the same as joeu2004's NPV.    Why not closer to zero?
It's a little hard to tell from the cash flows used.
With 25 values, what you really are solving for is a 24-degree polynomial.  (0-24)
It's easier to see if you re-arrange the equation.  The maximum values of the coefficient will be in the middle:

-184324775020759744 *r^12

This has 18 digits, and is larger than what a worksheet value can handle.  Plus, there are 6 surrounding values with 17 digits, etc.
Together, this is a good way to see how we are losing precision in the calculation.

There's more interesting math, but I'll leave that alone.
Hopefully, showing a loss of precision, and a near vertical slope will help explain why Excel's "not so great algorithm" might be having problems on a losing investment.

As a side note, with 25 values, the other valid solution is -1.936063358836872.
However, it's usually not worth mentioning in the analysis, which is that one doesn't earn their money back.

= = = =

HTH :>)

Dana

Many thanks Dana, some very interesting observations - particularly that iterations don't help. Still hard to see why a 1 cent change in one number in the billions can make IRR calculate or not. Something funny happening there!

I do have some positive aggregate cashflows with the same problem. Will check later today. Certainly this investment is not terrific (and will need subsidy)!

Dana wrote:

I can't add much

And yet you do. :-)  I was wondering when you would chime in. :-)

Dana wrote:

Excel 2016 returned a pretty accurate value for both the windows and Mac version.

Could you explain that in more detail?  Specially, what is your IRR formula that returned "pretty accurate" values?

Jon's issue is specifically that IRR(...,-0.05) [sic] and IRR(...,-0.0465377) [sic] do not work with the original large-valued cash flows, although they work when the small-valued cash flows (large divided by 1,000,000).

Are you saying that Jon's parameters work fine for you in Excel 2016?(!)

I'm surprised, because Jon's posting parameters claim that he is using Office 365, which I think includes Excel 2016 in some form.  (But of course, sometimes people do not enter the correct posting parameters.)

Dana wrote:

> ... "I increased the number of permitted iterations (to >1000) and the Maximum Change, with no effect."

If I am not mistaken, I don't believe IRR uses this option.  It uses it's own iteration.  Note from help:
"...until the result is accurate within 0.00001 percent. If IRR can't find a result that works after 20 tries, the #NUM! error value is returned."

That's what I thought, as well.  But https://support.office.com/en-us/article/How-to-correct-a-NUM-error-f5193bfc-4400-43f4-88c4-8e1dcca0428b (click here) claims otherwise.  And when an MVP mentioned it some time ago, I believe I tested and confirmed that it makes a difference sometimes.  Nevertheless, I confirmed that it seems to have no benefit for Jon's example.

Dana wrote:

What generally happens on the negative side of the x axis, (the rate), is that the slopes are usually very large.

[....]
If we look at the derivative of the equation at our solution of -.0465.., we see a slope of about -1.5 E12
[....]

When we divide the cash flows by 1,000,000 ,  we do not change the solution of r.  However, we do change the derivative by a large amount.  The new value is about -1.5 E6

That's the "inkling" I had.  Thanks for taking the time to explain it.

Also, for a given IRR close to the solution, the NPV for the large-valued cash flows is much larger than zero, whereas the NPV for the small-valued cash flows is less than zero.  For example:

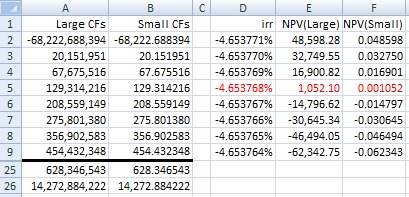
That might be problematic for the algorithm end-conditions.

Dana wrote:

An interesting side note is that if you plug your accurate value of r into the equation for cash flows, I get a value of 0.000082. This is basically the same as joeu2004's NPV.    Why not closer to zero?

[....]
With 25 values, what you really are solving for is a 24-degree polynomial.  (0-24)
[....] The maximum values of the coefficient will be in the middle:
-184324775020759744 *r^12
This has 18 digits

[....]

Together, this is a good way to see how we are losing precision in the calculation.

I agree that with the large-valued cash flows, even the best NPV is not as close to zero as we might like because of the loss of precision.  However, it is relatively close to zero, given the magnitude of the cash flows.

But I do not agree with your details.

The NPV equation is the sum of discounted terms of the form CF[i]/(1+r)^i.  By the way, i=1,..,25 according to the NPV help page, not 0,...,24 as we would expect.  That is one of the well-know caveats about using the NPV function.  Of course, I am assuming that the IRR function uses the equivalent of the NPV function internally.  We don't really know.

With that assumption, when r is between -4.65% (my guess) and the best solution, the discounted terms for the large-valued cash flows are between about -7E10 and 5E10, well within the calculation limitations of 64-bit binary floating-point.

Dana wrote:

As a side note, with 25 values, the other valid solution is -1.936063358836872.

IMHO, it is wrong to call any IRR "valid" if it is less than -100%, because the NPV equation is discontinuous at -100%.

Please forgive the nitpick.  But it irks me that Excel (X)IRR does return such misleading results sometimes.

Dana wrote:

There's more interesting math, but I'll leave that alone.

Since when has that ever stopped you. :-)

Seriously, good analysis.  I hope it is helpful to Jon.  (Albeit of little comfort, perhaps.)

> .. Could you explain that in more detail?  Specially, what is your IRR formula that returned "pretty accurate" values?

> .. Are you saying that Jon's parameters work fine for you in Excel 2016?(!)

Yes.  Using Excel 2016, I just used =IRR() on his data "without" a guess, and it returned a value without an error.

It seems to check out using Excel vba, and I checked vba with another program (using a precision of 50)

1.  Excel IRR(),  2.  Simple vba,  3.  Other program at precision 50

 -0.0465376793361623                                    'IRR()
 -0.0465376793361622074709165174                        'Simple Excel VBA
 -0.046537679336162207470916517445170369653953185594472 'Other